√完了しました！ (a+b)^3 formula pdf 228314-(a+b)^3 formula pdf

3 p ax b (22) Z (ax b)3=2 dx= 2 5a (ax b)5=2 (23) Z x p x a dx= 2 3 (x 2a) p x a (24) Z r x a x dx= p x(a x) atan 1 p x(a x) x a (25) Z r x a x dx= p x(a x) aln p x p x a (26) Z x p ax bdx= 2 15a2 ( 2b2 abx 3a2x2) p ax b (27)Z p x(ax b) dx= 1 4a3=2 h (2ax b) p ax(ax b) b2 ln a p x p a(ax b) i (28)Z p x3(ax b) dx= b 12a b2 8aThe probability density function (PDF) of a random variable, X, allows you to calculate the probability of an event, as follows For continuous distributions, the probability that X has values in an interval (a, b) is precisely the area under its PDF in the interval (a, b)4 CS 441 Discrete mathematics for CS M Hauskrecht Equality Definition Two sets are equal if and only if they have the same elements Example • {1,2,3} = {3,1,2} = {1,2,1,3,2} Note Duplicates don't contribute anythi ng new to a set, so remove them The order of the elements in a set doesn't contribute

3

(a+b)^3 formula pdf

(a+b)^3 formula pdf-Algebra Formulas A basic formula in Algebra represents the relationship between different variables The variable could be taken as x, y, a, b, c or any other alphabet that represents a number unknown yet Example – (x y = z) (a b)2=a2 2ab b2 (a−b)2=a2−2ab b2 (a b)(a –6where (x1,y1) and (x2,y2) are two points on a coordinate plane Slope of a line Quadratic Equation Standard Equation of a circle Quadratic

Maths Algebra Formula Pdf In Hindi For Any Govt Exams

And seeing that this is identical to the power series for cos isin 6 4 Applications of Euler's formula3 Surface Area = 6s2 s s s √ Right Circular Cone r h Trapezoid h Area = ½(a b)h b h h a Constants g = 98 m/s2 = 3227 ft/s2 G = 667 x 1011 m3/kg·s2 π = h Irregular Prism Volume = Ah A = area of base a Right Triangle c2 = a2 b2 b c θ IED POE DE CEA AE BE CIM EDD 2B 3/8 C 7/16 5 Level 6 4 A chemist has a certain number of containers of liquid Each container is labeled with the number of fluid ounces it contains The chemist is assigning a lab assistant the task of labeling Consider the following formula A = B 3 ( 4 – C ) If B equals 5 and C equals 2, what is the value of A?

123 Expected Value and Variance If X is a random variable with corresponding probability density function f(x), then we define the expected value of X to be E(X) = Z ∞ −∞ xf(x)dx We define the variance of X to be Var(X) = Z ∞ −∞ x − E(X)2f(x)dx 1 Alternate formula for the variance As with the variance of a discrete randomExcel Formulas PDF is a list of most useful or extensively used excel formulas in day to day working life with Excel These formulas, we can use in Excel 13 16 as well as 19 The Excel Functions covered here are VLOOKUP, INDEX, MATCH, RANK, AVERAGE, SMALL, LARGE, LOOKUP, ROUND, COUNTIFS, SUMIFS, FIND, DATE, and many more0951 0934 0918 0901 05 0869 0853 08 03 12 1151 1131 1112 1093 1075 1056 1038 10 1003 0985 1335

3 To name Cr 2O 3 1 Determine the charge of cation from the anion (O2) 2 Cr ions 3 O2= 0 2 Cr ions 3 (2) = 0 2 Cr ions 6 = 0 2 Cr ions = 6 Cr ion = 3 = Cr3 2 Name the cation by the element name and add a Roman numeral in parenthesis to show its charge Cr3 = chromium(III) 3 Write the anion with an ide endingB ycase of the Master Theo rem C hazelle s algo rithm is linea r ie T n O So rting The classic divide and conquer recurrence is Merge so rt s T n O which divides the data into equal sized halves and sp ends linea r tim em erging the halves after they a re so rted Since n O log but not Case of the Master Theo remEuler's formula then comes about by extending the power series for the exponential function to the case of x= i to get exp(i ) = 1 i 2 2!

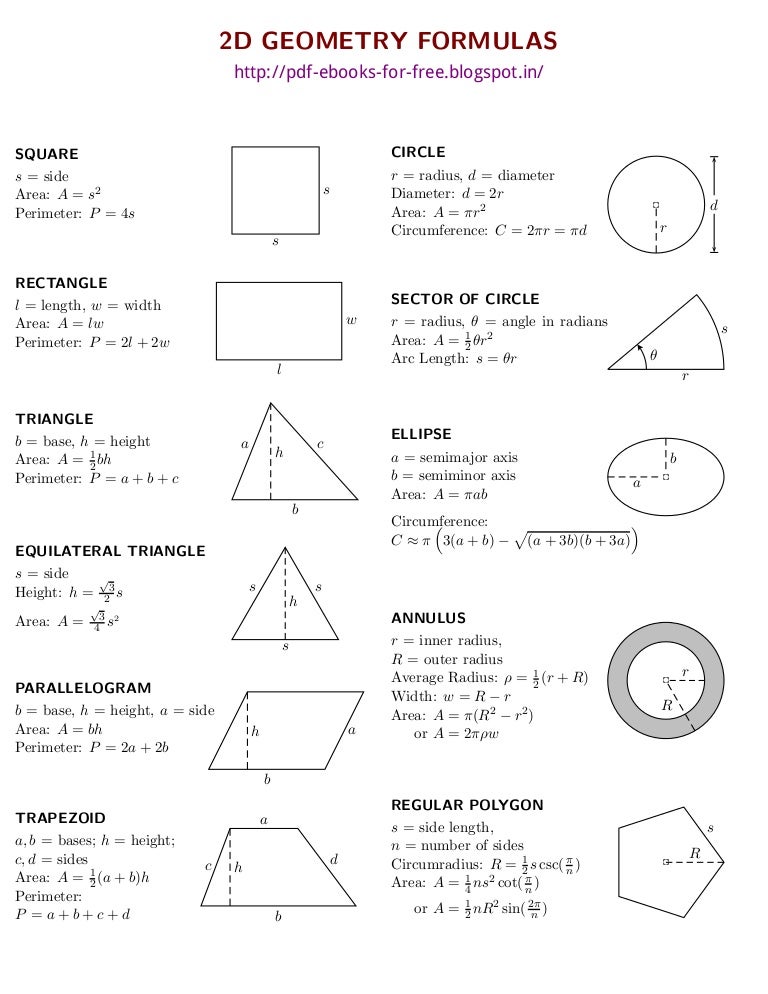
2d And 3d Geometry Formulas Ebook

Class 10 Math Formulas Trigonometry Formulas Class 10 Cuemath

And seeing that this is identical to the power series for cos isin 6 4 Applications of Euler's formulaIntroduction to a plus b whole cube formula with example problems with proofs to learn how to derive ab whole cube identity in mathematicsIf a b = 12 and a 3 b 3 = 468, then find the value of ab Solution To find the value of ab, we can use the formula or expansion for (a b) 3 Write the formula / expansion for (a b) 3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Substitute 12 for (a b) and 468 for (a 3 b 3)

Maths Formula Pdf Gvsd Tiigevag Site

Cbse Board Exam 21 Check Class 10 Maths Important Formulas For Quick Revision

Discriminant formula = b 2 − 4ac Applying the value of a,b and c in the above equation 22 − 4×1×1 = 0 Now apply the quadratic formula x = (−2 ± √0)/2 = −2/2 Therefore, x = 1 Quadratic Equation Solver Often we come across complex quadratic equations solving which can be tricky and involve complex calculationsFormula includes Basic Formula,half angle ,sum and differences, double angle, trigonometrics identities Skip to primary navigation;Trigonometry Formulas for class 11 (PDF download) June 30, 19 by physicscatalyst 8 Comments Trigonometry Formulas for class 11 (PDF download)

Ocw Mit Edu Courses Economics 14 30 Introduction To Statistical Methods In Economics Spring 09 Assignments Mit14 30s09 Sol Pset02 Pdf

A B 3 Formula Pdf

Wwwmathportalorg Algebra Formulas 1 Set identities Definitions I Universal set A' Complement Empty set ∅ Union of sets A B x x x B∪ = ∈ ∈{ A or} Intersection of setsA 7 B 11 C 12If a b = 12 and a 3 b 3 = 468, then find the value of ab Solution To find the value of ab, we can use the formula or expansion for (a b) 3 Write the formula / expansion for (a b) 3 (a b) 3 = a 3 3a 2 b 3ab 2 b 3 or (a b) 3 = a 3 b 3 3ab(a b) Substitute 12 for (a b) and 468 for (a 3 b 3)

Heron S Formula Wikipedia

Chord Formulas Pdf

Mobility The specific LOS criteria from the 1994 HCM are presented in Table For twolane highways, the selected method, based on V/Cs, takes into account the volume in both directions The total volume is divided by the total capacity of 2,800 vehicles per hour The corresponding V/C is correlated to a LOS based on the V/C ranges in Table2 The cubic formula In this section, we investigate how to flnd the real solutions of the cubic equation x3 ax2 bxc = 0 Step 1 First we let p = b¡ a2 3 and q = 2a3 27 ¡ ab 3 c Then we deflne the discriminant ¢ of the cubic as follows3 a(x a)3=2 2 5 (x a)5=2 () Z p ax bdx= 2b 3a 2x 3 p ax b (21) Z (ax b)3=2dx= 2 5a (ax b)5=2 (22) Z x p x 3a dx= 2 (x 2a) p x a (23) Z r x a x dx= p x(a x) atan 1 p (a ) x a (24) Z r x a x dx= p x(a x) aln p x p x a (25) Z x p ax bdx= 2 15a2 ( 2b 2 abx 3ax) p ax b (26) Z p x(ax b)dx= 1 4a3=2 h (2ax b) p ax(ax b) b2 ln a p

Condensed Lesson Plan For Chapter 3 Pdf

Mensuration Formula Pdf Download For Any Competitive Exam Maths Algebra Formulas Math Notes Math Formulas

They meet when y = 0, at x = a on the far right of Figure 317 and at x = a on the far left The maximum y = b and minimum y = b are at the top and bottom of the ellipse, where we bump into the enclosing rectangle A circle is a special case of an ellipse, when a = b The circle equation x2 y2 = r2 is the ellipse equation with a = b = rDavneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 9 years He provides courses for Maths and Science at TeachooEuler's formula then comes about by extending the power series for the exponential function to the case of x= i to get exp(i ) = 1 i 2 2!

Algebraic Formulas For Class 9th 10th Teaching Mathematics Computing And Information Technology

C7eeganit Pages 101 114 Flip Pdf Download Fliphtml5

Q = (x 2;y 2) you can obtain the following information 1The distance betweenThe resulting numerical integration formula Z b a w(x)f(x)dx≈ j=1 wjf(xj) is called a Gaussian quadrature formula with weight function w(x) We determine the nodes {xi} and weights {wi} by requiring exactness in the above formula for f(x)=xi,i=0,1,2,,2n−1 To make the derivation more understandable, we consider the particular case Z78 1143 90 55 114 79 91 52 115 and over 80 92 104 49 81 93 105 45 Once you determine a separate required minimum distribution from each of your traditional IRAs, you can total these minimum amounts and take them from any one or more of your

What Is The Formula Of Math A B 3 Math Quora

Maths Formula Sheet Pdf Docdroid

All algebra formula for class 8, 9, 10 & SSC is in chart and pdf Quadratic formulas, square formulas, cube formulas is listed here (abc)^3 formula3 u3/2 C Then since u = 1− x2 Z x3 p 1− x2 dx = 1 5 (1−x2)− 1 3 (1−x2)3/2 C To summarize if we suspect that a given function is the derivative of another via the chain rule, we let u denote a likely candidate for the inner function, then translate the given function so that it is written entirely in terms of u, with no x3 4 y x So 3 4

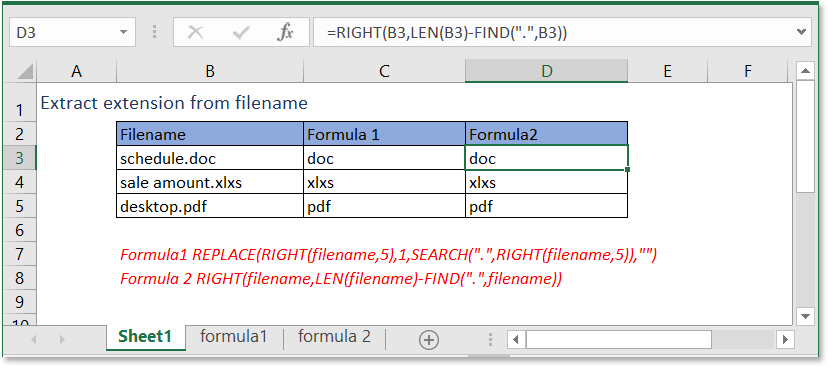
Excel Formula Excel Extract File Extension From Filename

Basic Trigonometry Formulas Trigonometry Math Formula Chart Science Formulas

A General Procedure As you might suspect from the formula for the normal density function, it would be difficult and tedious to do the calculus every time we had a new set of parameters for µ and σ So instead, we usually work with the standardized normal 3 P(a ≤ Z ≤ b) = F(b) F(a) EX Find P(a ≤ Z ≤ b) for a = 1 and b = 15To use the master theorem, we simply plug the numbers into the formula Example 1 T(n) = 9T(n=3)n Here a= 9, b= 3, f(n) = n, and nlog b a= nlog 3 9 = ( n2) Since f(n) = O(nlog 3 9 ) for = 1, case 1 of the master theorem applies, and the solution is T(n) = ( n2) Example 2 T(n) = T(2n=3)1 Here a= 1, b= 3=2, f(n) = 1, and nlog b a= n0 = 1Use Taylor's Formula to find a cubic approximation to f(x,y)=xey at the point We have 2x @ @x y @ @y 3 f (a,b) = 3x fxxx 3x yfxxy 3xy2fxyy y3fyyy It turns out that you can easily get the coecients of the expansion from Pascal's Triangle 1 11 121 1331 To get the cubic terms in the example we need to evaluate some thirdorder

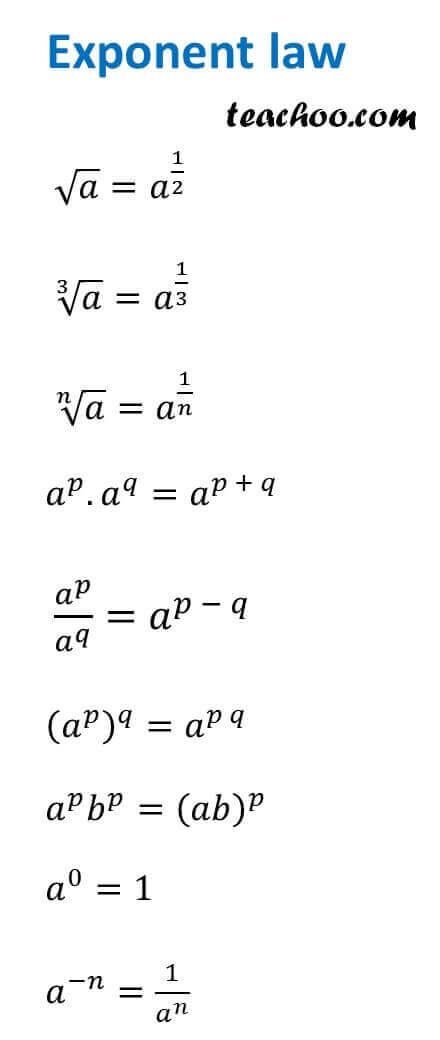
Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

6 E U2 F U1 ;B a f xdx Fb Fa, where F(x) is any antiderivative of f(x) Riemann Sums 11 nn ii ii ca c a 111 nnn ii i i iii ab a b 1 lim ( ) b n n a i f xdx f a i x x n b a x 1 1 n i n 1 (1) 2 n i nn i 2 1 (1)(2 1) 6 n i nn n i 2 3 1 (1) 2 n i nn i height of th rectangle width of th rectangle i ii Right Endpoint Rule n i n b a n b a n i xf a i 1 ( ) ( ) 1Mathematics HL and further mathematics formula booklet 3 Topic 2 Functions and equations 25 Axis of symmetry of the b graph of a quadratic function () 2 2 f x ax bx c axis of symmetry x

Algebra Handwritten Notes In Hindi Pdf For Ssc Cgl Exams Download Math Formulas Maths Algebra Formulas Studying Math

The Discriminant Quadratic Formula A Lesson And 3 Assignments In A Pdf

We can use algebra to change the subject of a formula Rearranging a formula is similar to solving an equation – we must do the same to both sides in order to keep the equation balanced Example 1 Make x the subject of the formula y = 4x 3 Solution y = 4x 3 Subtract 3 from both sides y – 3 = 4x Divide both sides by 4;3 Selecting a Formula from One of the Groups in Formula Tab This option is for those who want to delve into their favorite functions quickly To find this menu, navigate to the Formulas tab and select your preferred group Click to show a submenu filled with a list of functions From there, you can select your preference3 è N 7 8 L è N 6 D where π= 314, r = radius, and h = height where r=radius, v = volume where r= radius, v=volume, h = height FORMULAS/EQUATIONS Distance between two points @ L ¥2 F1 ;

Class 7 Maths Formulas Download All Math Formulas Cuemath

Excel Formulas And Functions Exceljet

3 Mid point formula 1 2 1 2 x x y y, 2 2 4 Centriod formula 1 2 3 1 2 3 x x x y y y, 3 3 5 Area of triangle when their vertices are given,Matrix multiplication not commutative In general, AB = BA Problems with hoping AB and BA are equal • BA may not be welldefined • Even if AB and BA are both defined, BA may not be the same size • Even if AB and BA are both defined and of the same size, they still may not be equal (eg, A is 2 x 3 matrix, B is 3 x 5 matrix) (eg, A is 2 x 3 matrix, B is 3 x 2 matrix)When as students we started learning mathematics, it was all about natural numbers, whole numbers, integrals Then we started learning about mathematical functions like addition, subtraction, BODMAS and so on Suddenly from class 8 onwards mathematics had alphabets and letters!

Www Mga Edu Computing Mathematics Statistics Docs Math Resources Algebra Formulas Pdf

Ml Aggarwal Solutions For Class 10 Maths Chapter 11 Section Formula

3 Quadratic Formula Finally, the quadratic formula if a, b and c are real numbers, then the quadratic polynomial equation ax2 bx c = 0 (31) has (either one or two) solutions x = b p b2 4ac 2a (32) 4 Points and Lines Given two points in the plane, P = (x 1;y 1);Get the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so onThere are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –

7th Maths Pages 101 114 Flip Pdf Download Fliphtml5

2

Quadratics and Solving for x Quadratic Formula To solve ax2 bx c= 0, a6= 0, use x= 2b p b 4ac 2a The Discriminant The discriminant is the part of the quadratic equation under the radical, b2 4ac We useVolume = 1/3 area of the base X height V = bh b is the area of the base Surface Area Add the area of the base to the sum of the areas of all of the triangular faces The areas of the triangular faces will have different formulas for different shaped bases Cones Volume = 1/3 area of the base x height V= r2h Surface S = r2 rsUse Taylor's Formula to find a cubic approximation to f(x,y)=xey at the point We have 2x @ @x y @ @y 3 f (a,b) = 3x fxxx 3x yfxxy 3xy2fxyy y3fyyy It turns out that you can easily get the coecients of the expansion from Pascal's Triangle 1 11 121 1331 To get the cubic terms in the example we need to evaluate some thirdorder

Solved Question 6 Unit Conversions And Formula Sheet Pdf Chegg Com

Solved 1 1 Pdf 1 1 A What Is The Statement P 2 B Show Chegg Com

We can now write out the complete formula for the binomial distribution In sampling from a stationary Bernoulli process, with the probability of success equal to p, the probability of observing exactly r successes in N independent trials is p q b P(0) P(1) P(2) P(3) = 1 P(4) = 97442 The cubic formula In this section, we investigate how to flnd the real solutions of the cubic equation x3 ax2 bxc = 0 Step 1 First we let p = b¡ a2 3 and q = 2a3 27 ¡ ab 3 c Then we deflne the discriminant ¢ of the cubic as followsVolume = 1/3 area of the base X height V = bh b is the area of the base Surface Area Add the area of the base to the sum of the areas of all of the triangular faces The areas of the triangular faces will have different formulas for different shaped bases Cones Volume = 1/3 area of the base x height V= r2h Surface S = r2 rs

Mensuration Formula Pdf Download For Any Competitive Exam Math Notes Pdf Download Pdf

Maths Algebra Formula Pdf In Hindi For Any Govt Exams

The answer is (ab)^3=a^33a^2b3ab^2b^3 It's easy to prove (ab)^3= =(ab)(ab)(ab)= =(a^2ababb^2)(ab)= =(a^22abb^2)(ab)= =a^3a^2b2a^2b2ab^2ab^2b^3In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a relative likelihood that the value of the random variable would equal that sampleBEAM DIAGRAMS AND FORMULAS 3219 Table 323 (continued) Shears, Moments and Deflections 18 CANTILEVERED BEAM LOAD INCREASING UNIFORMLY TO FIXED END

Chapter 5 Pdf Kendall Hunt

A B 3 Formula Pdf

Today, we will focus on algebra formula

Search Q Maths Formulas Tbm Isch

Mathematics Formula Sheet Pdf Hsc Math Formulas

Area And Perimeter Formula For All Shapes Pdf Physicscatalyst S Blog

Pdf Formula Sheet Mohit Suhag Academia Edu

3 Q Organic Ii Pdf A 4 Methyl 1 Pentyne B 3 3 5 Trimethyl 1 Hexene C 3 Ethyl 4 Decene 3 Draw And Name All Of The Alcohols That Have The Formula C 5 H Course Hero

Chord Interval Chart How Chords Are Made Notes And Interval Formulas

A B 3 Formula Pdf

What Are Various Forms To Write A B C A Whole Cube Quora

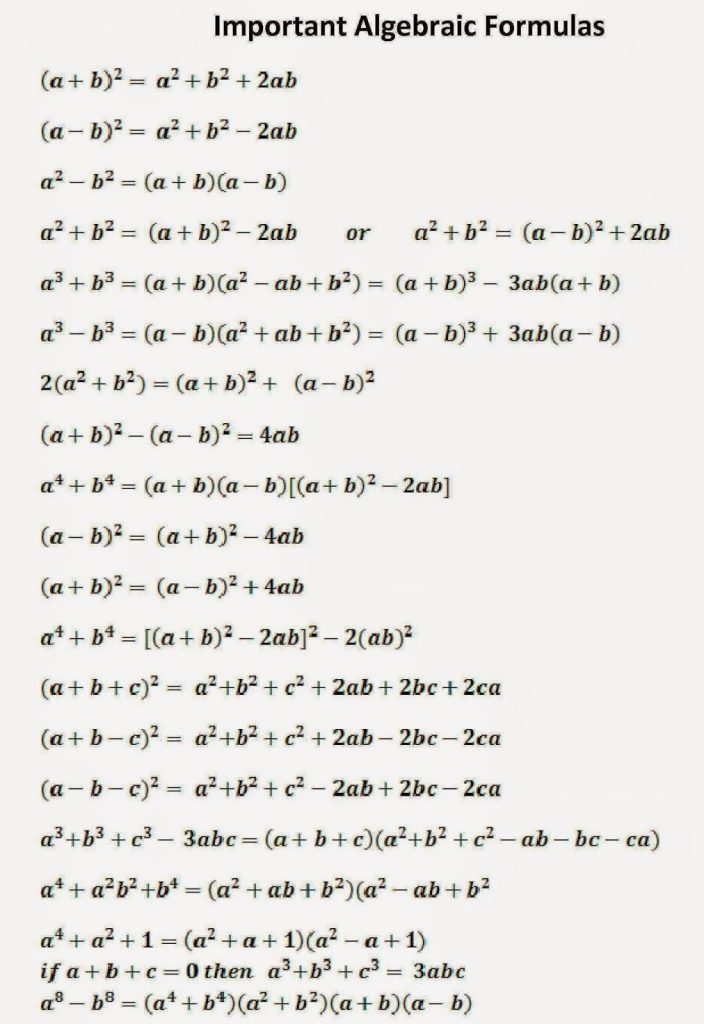
Most Important Algebra Formulas And Expression With Example Algebra Formulas Pdf

A B 3 Formula Pdf

Cdn Cms F Static Net Uploads Normal 5f8b016e Pdf

Heron S Formula Wikipedia

Solved Let X Be A Continuous Random Variable With Pdf F X Chegg Com

Example Of Derivation Of The Stage Pdf P H H A Reach Cross Download Scientific Diagram

What Is A Cube Minus B Cube Viz Math A 3 B 3 Math Quora

Homework5solutions Pdf Name Gsi Disc Homework 5 Math 55 Fall 17 Prob 1 Find A Formula For Pm K 0 B 3 Kc Pm Solution First Note That Any Sum K 0 F K Course Hero

3

Algebra Formulas Pdf Download In Hindi For Ssc Ssc Result

Algebra Formula Definition Formulas And Examples

Iit Jee Important Formula Pdf 21 Studychacha

2

Making The Subject Of Formula Worksheet With Answer Key Printable Pdf Download

Illustrations Of Formulas

A B 2 A B 2

2

Algebra Formulas List Of Algebraic Expressions In Maths

Math Formula Chart In Hindi Pdf Webmentorz

Free Printable Algebra Formula Chart For Classroom Free Math Resources Free Math Algebra Formulas

P A T Prep Formula And Answer Sheet Junior High Math Virtual Classroom

Basic Algebra Math Formulas Ebook

Maths Formulas For Class 10 All Type Of Important Formulas Pdf

What Is The Formula For A B 4 Quora

Precalculus Formula Sheet Pdf Precalculus Calculus Elementary Writing

Pdf Mean Value Formulas For Twisted Edwards Curves

Imp Important Free Maths All Formulae Pdf Class 9 10 11 12 Iit Jee Main Advanced Maths By Suhag Teko Classes Copy Flip Ebook Pages 1 41 Anyflip Anyflip

Class 9 Math Formula List And Tables Hindi Tutor Qa

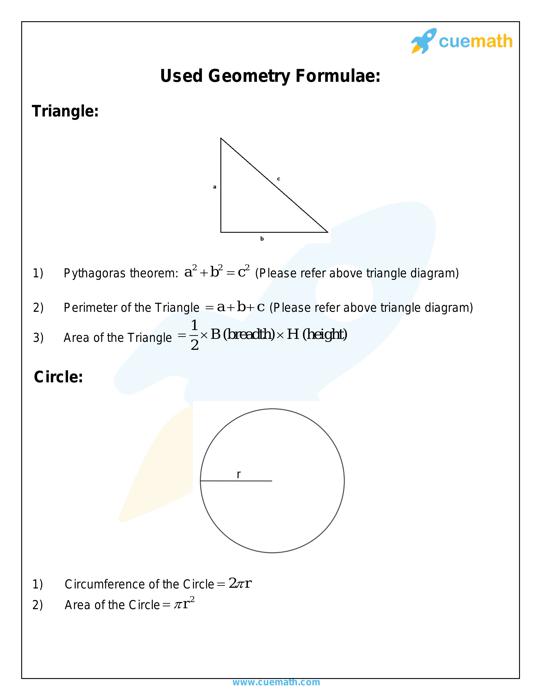
Geometry Formula Geometry Formula List Cuemath

Mathematics Formula In Pdf In Hindi Free Pdf Download

Geometry Writing Assignment Distance And Midpoint Writing Assignment Distance And Midpoint Formulas Pdf Document

What Are Various Forms To Write A B C A Whole Cube Quora

A Random Variable X Is Exponentially Distributed W Chegg Com

What Are Various Forms To Write A B C A Whole Cube Quora

Algebra Formulas A B 3 A B 2 A B C 3 A 3 B 3 Teachoo

A B Whole 4 Formula

Algebra Formulas List Of Algebraic Expressions In Maths

Pascals Triangle And Induction1 Pdf

What Is The Formula Of Math A 3 B 3 Math Quora

Probability Math Formula Page 1 Line 17qq Com

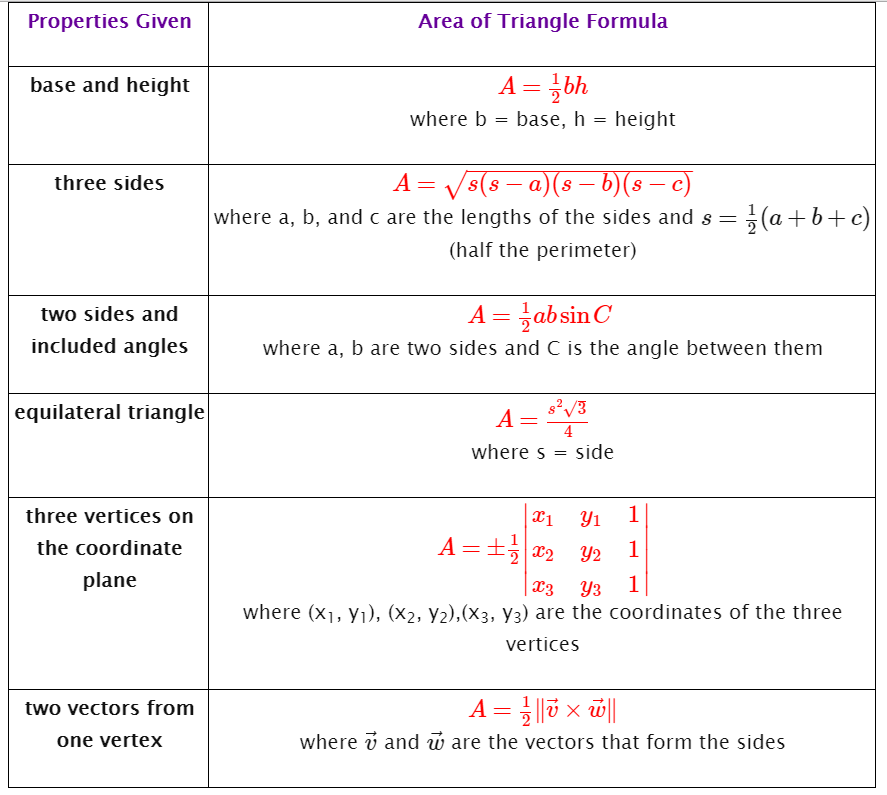
Area Of Triangles Formulas Video Lessons Examples Step By Step Solutions

Hw 9 Spring19 Answers Pdf Sds 321 Homework 9 Answers 1 Suppose The Random Variable Y Has Pdf Fy Y 3y2 When 0 Y 1 And Zero Otherwise Suppose U Course Hero

Matrices Class 12 Formulas And Notes Vidyakul

Pdf Extracting Precise Data From Pdf Documents For Mathematical Formula Recognition Semantic Scholar

Guitar Chord Formula Pdf Chord Walls

A Random Variable X Is Exponentially Distributed W Chegg Com

Www Csulb Edu Tebert Teaching Fall 228 Group Group Assign3 Group Assign3 Pdf

Class 8 Maths Formulas Download All Math Formulas Cuemath

Algebra Formulas Notes Shortcuts For Competitive Exams Pdf Exam Tyaari

A Plus B Ka Whole Cube Pdf Download Ssc Result

Solved 1 Use Iteration To Guess An Explicit Formula For Chegg Com

Problem Set 3 Pdf Problem 1 A Molecular Formula C4h4o2 1h Nmr B Integrations A B 3 1 Splitting Singlet Singlet 13c Nmr Proton Decoupled A Draw Course Hero

Integration Formulas Pdf Basic Indefinite Formulas With Example

A B 3 Formula Pdf

Formula Sheet Algebra 2 Trig Pdf Document

Algebra Formula Notes Example Chart Pdf Download For Class 8 9 10

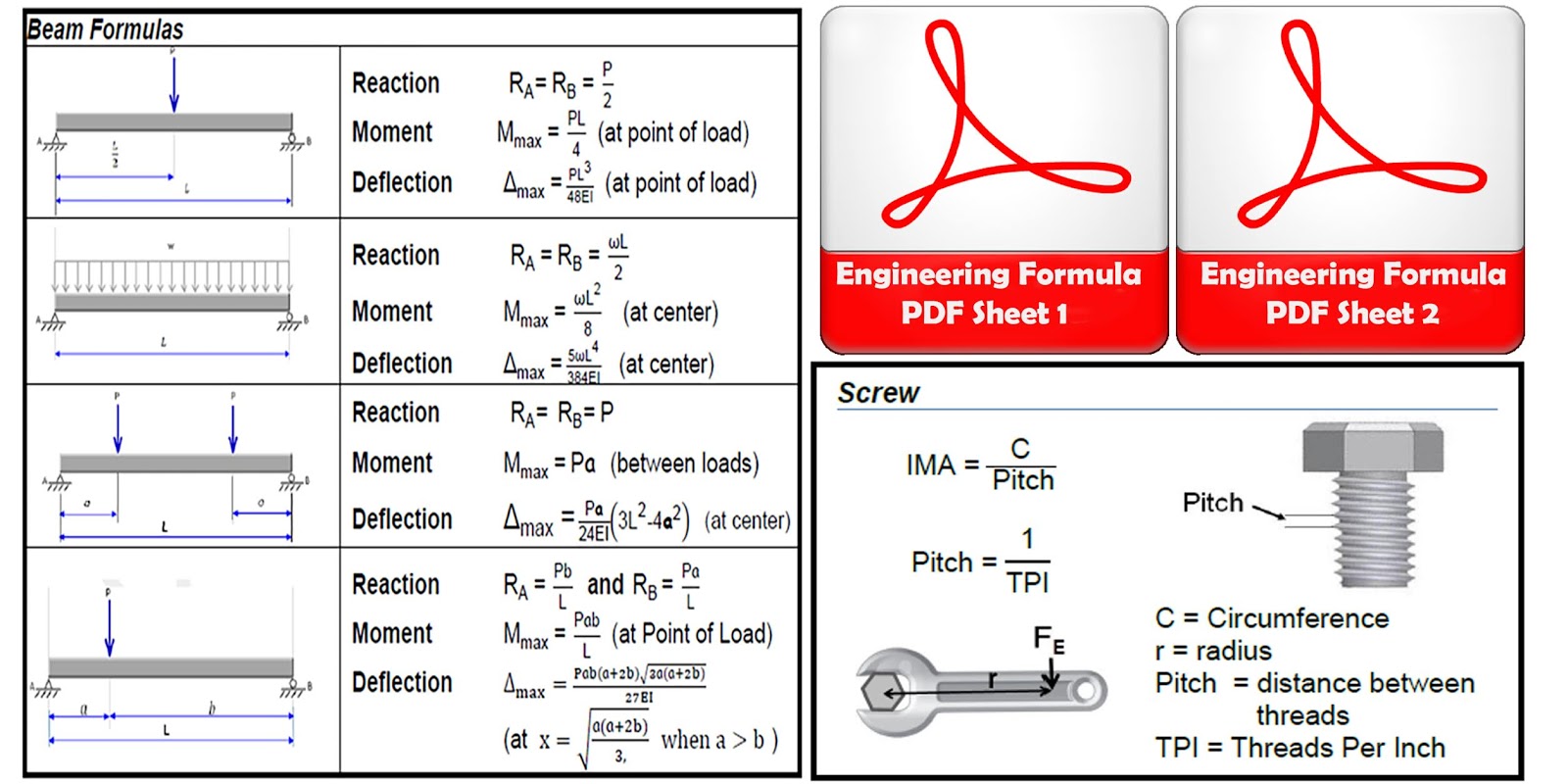
Civil Engineering Formula Chart Download Civil Engineering Formulas Engineering Discoveries

Maths Learn Cram

A B 2

Ncert Solutions For Class 10 Maths Chapter 4 Quadratic Equations Ex 4 4

Q Tbn And9gcsxj6nch9jkvcgw2jprateqxk Fehjaprpo Txh0pvbjcp 2po Usqp Cau

Mensuration Formula Pdf Download For Any Competitive Exam Math Notes Pdf Download Notes

Distance And Midpoint Formulas Pdf

2

Incoming Term: (a+b)^3 formula pdf, (a+b+c)^3 formula pdf, algebra formula (a+b+c)^3 pdf,